Docs

位置情報ゲームの移動検証について

乱文

人類は，移動を進化させてきました．歩いたり走ったりしていた時代から，馬車や自転車が発明され，汽車や自動車が開発され，電車や新幹線が敷設されました．

例えばゲーム内の要素について，場所のフラグをとる要素があったとします．このようなゲームシステムは，例えば，駅メモ - ステーションメモリーズ！ - や Swarm（Swarm をゲームと呼ぶのかは諸説ありますが）にあります．これらは，自身がいくら移動したかに価値が見受けられます．

さて，スマートフォンは位置情報を取得することができます．そして，ゲームサーバには，取得した緯度・経度の情報あるいは周辺施設の情報を送信します．しかし，その情報は実際にセンサを利用して取られたものであると証明することはできません．Google 検索などで，「【特定のゲーム名】 位置情報　偽装」などと調べると，様々な形で位置情報を偽装する方法が出てきます．この方法を取れば，５分前まで札幌の時計台にいたはずなのに，今何故か沖縄の首里城付近にいるなどといった芸当が可能になるわけです．

このように，位置情報の偽装を完全に防ぐことは諦めたほうが良いでしょう．しかし，２点以上の位置情報があれば，矛盾は検出できるかもしれません．今回はその方法を考察していきます．

距離を計算する

２点間の位置を把握し，距離を求めます．などと簡単に言ってはいますが，地球は球面なので，単純に平面で三平方の定理を利用するようには行きません．

簡単な方法として，Hubenyの公式を挙げてみましょう．

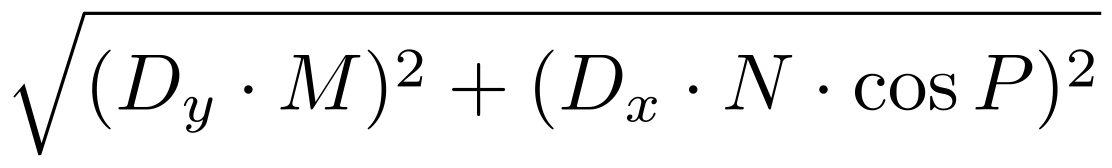
これは，次の図のような原理で計算できます．

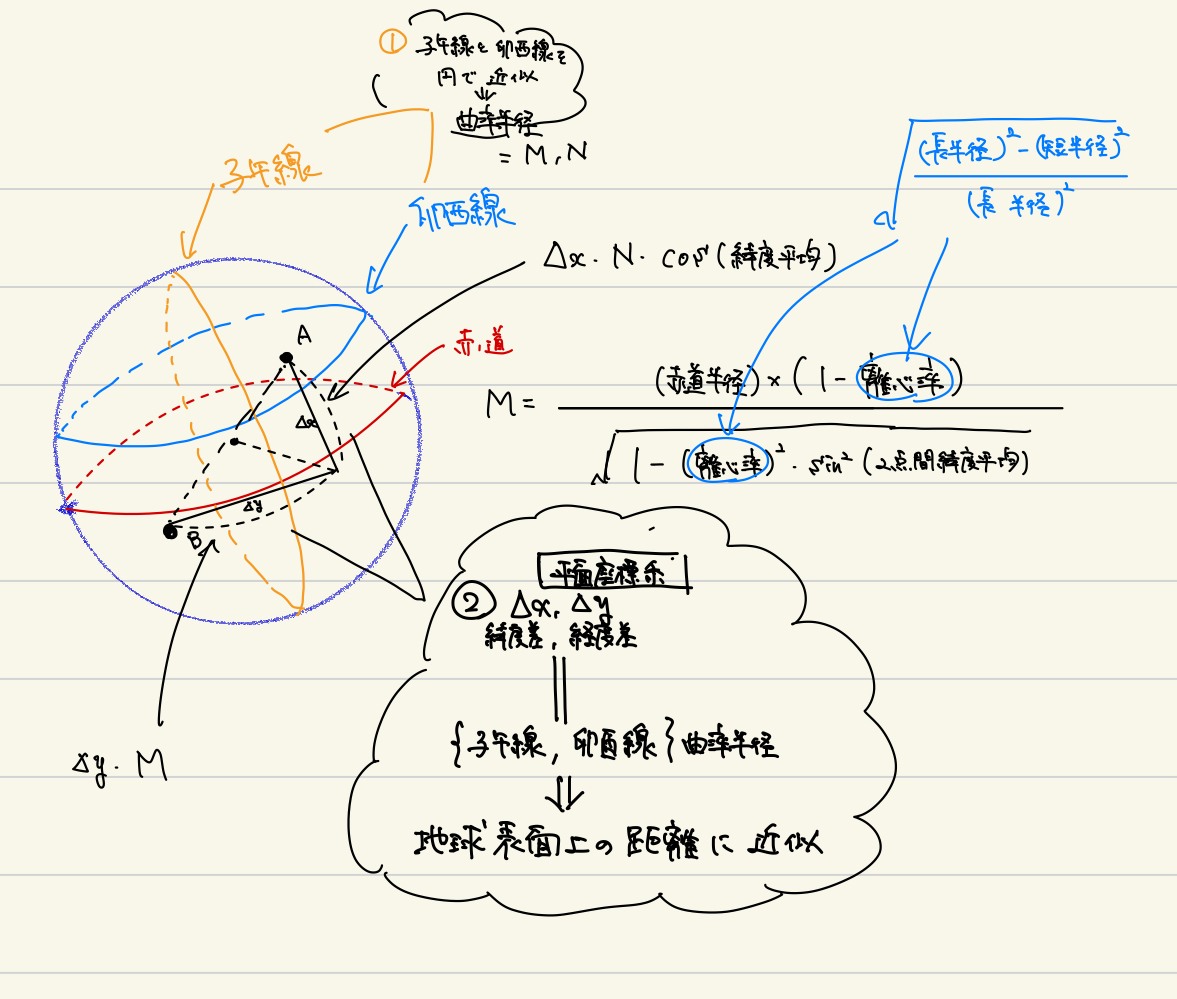
まず，子午線と卯酉線は，球面上（楕円球上）にあるため，その断面をほどんど円として近似できます．この円の半径をそれぞれ，子午線曲率半径 M，卯酉線曲率半径 N と呼びます．

次に，緯度や経度は座標平面上の概念であるため，緯度・経度の差を弦ととらえて，地球上の距離である弧の距離を求めます．

最後に，三平方の定理から最初の距離を割り出します．確かに地球は球面なので多少の誤差は出ますが，問題とするほどではない誤差でしょう．注意するべきは与えられた数値は弧度法であるため，ラジアンに変換しなければならない点です．

これを Go で実装するとこんな感じ．といっても，ただ公式を並べただけです．

import (
	"fmt"
	"math"
)

func getDistanceWithHubeny(y1 float64, x1 float64, y2 float64, x2 float64) float64 {
	// (緯度1, 経度1, 緯度2, 経度2)
	Rx := 6378137.000    // 長半径（測地系: WGS84）
	Ry := 6356752.314245 // 短半径（測地系: WGS84)
	P := (y1 + y2) / 2
	E := math.Sqrt(
        (math.Pow(Rx, 2) - math.Pow(Ry, 2)) / math.Pow(Rx, 2)
        ) // 離心率
	W := math.Sqrt(1 - math.Pow(E, 2)*math.Pow(math.Sin(P), 2))
	M := Rx * (1 - math.Pow(E, 2)) / math.Pow(W, 3) // 子午線曲率半径
	N := Rx / W                                     // 卯酉線曲率半径

	// 度からラジアンへ
	y1 = y1 * math.Pi / 180
	x1 = x1 * math.Pi / 180
	y2 = y2 * math.Pi / 180
	x2 = x2 * math.Pi / 180

	dx := x2 - x1
	dy := y2 - y1

	D := math.Sqrt(math.Pow(dy*M, 2) + math.Pow(dx*N*math.Cos(P), 2))

	return D
}

func main() {
	// 札幌 (43.0620 / 141.3544)
	// 那覇 (26.1245 / 127.4052)
	d := getDistanceWithHubeny(43.0620, 141.3544, 26.1245, 127.4052)
	fmt.Println(d)
}

実行結果は，2.432252139063118e+06 になりました．2.4×10^6 [m] ですから，割と妥当な値が出たのではないでしょうか．

その他にも，距離を計算する方法には，以下のようなものがあります．

距離の実装ライブラリ

なお，今回は不正検知が目的のため，距離の誤差がそこまで重要になることはないはずなので自分で実装しても良いでしょう．しかし，実際の開発では，距離計算に正確な数値が必要となる場面があるかもしれません．

その時は，次のライブラリが役に立つでしょう．車輪の再開発は，実運用上おすすめしません．

どれぐらいの速度の地上移動が，人間として現実的か

鉄道（新幹線）の速度は，Wikipedia によると，2024年で東北新幹線の 320 [km/h] だそうです．しかし，新幹線は駅で停車したり，カーブで減速します．例えば，東京から博多までの営業キロは 1069.1 [km] です．この間ののぞみの所要時間は最短で4時間52分です．これを基にすると，おおよそ 220 [km/h] 程度でしか，人類は移動できないことと，おおよそ推測できます．

加えて，先程の距離計測は，直線距離の話です．人間が行き来するのは道路ですから，直線距離よりもロスが生じます．このロスを含んだ道路上の距離を学術的には「迂回距離」と呼ぶそうです．直線距離を 1 とした場合における迂回距離の比を示す指標を迂回率と呼びますが，田村ら(2001)の論文によれば，高速道である常磐自動車道の迂回率は東名道は 1.000, 関越道は 1.318, 東北道は 1.851 となっています．さらに，筑波研究学園都市の迂回率は 1.25 程度とされています．このように，はっきり言ってまちまちであるため，迂回率の数値はサービスなどを開始したあとに，調整していくしかないと思われます．

結論

上の事項を懸案したうえで，私であれば以下のように実装します．単位は [km/h] です

加えて，API のレートリミットなどが必須でしょう．この計算式では，近場の不正は，見抜くことができませんが，1秒に複数回リクエストが投げられるほどの移動は，人類にはまだできません．

おわりに

実際の開発現場では，どのように対処しているのでしょうか．

ご存じの方は，教えてくだされば幸いです．

参考文献

Published at